Задача
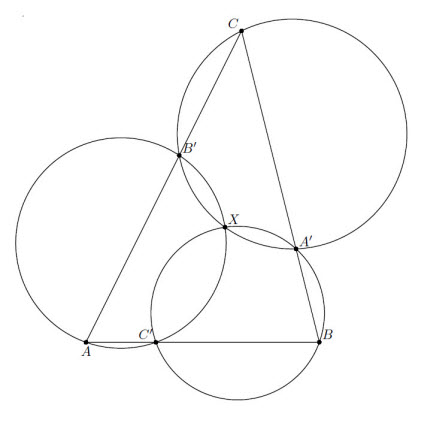
Точки A', B', C' лежат на сторонах BC, CA, AB треугольника ABC. Точка X такова, что ∠AXB = ∠A'C'B' + ∠ACB и ∠BXC = ∠B'A'C' + ∠BAC.
Докажите, что четырёхугольник XA'BC' – вписанный.
Решение
Пусть Y – отличная от C' точка пересечения окружностей AB'C' и BC'A'. Тогда, так как ∠B'YC' = 180° – ∠BAC и ∠C'YA' = 180° – ∠CBA, то
∠A'YB' = 180° – ∠ACB, то есть точка Y лежит также на описанной окружности треугольника CA'B'. Заметим теперь, что
∠AYB = ∠AYC' + ∠C'YB = ∠AB'C' + ∠C'A'B = 360° – ∠C'B'C – ∠CA'C' = ∠ACB + ∠A'C'B' = ∠AXB (см.рис.). Аналогично ∠BYC = ∠BXC, то есть точки X и Y совпадают.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет