Задача
Дан прямоугольный треугольник ABC с прямым углом C. Пусть BK – биссектриса этого треугольника. Описанная окружность треугольника AKB пересекает вторично сторону BC в точке L. Докажите, что CB + CL = AB.
Решение
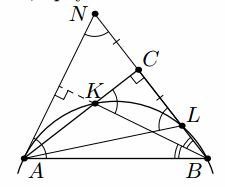
Решение 1: Отложим на продолжении BC за точку C отрезок CN = LC. Надо доказать, что AB = NB.
Так как четырёхугольник ABLK вписан, ∠CKB = 180° – ∠ALB = ∠ALC (рис. слева). С другой стороны, прямоугольные треугольники ACL и ACN равны по двум катетам, так что ∠ANC = ∠ALC = ∠CKB = 90° – ½ ∠B. Тогда из треугольника ABN имеем
∠BAN = 180° – ∠B – ∠ANB = 180° – ∠B – (90° – ½ ∠B) = ∠ANB. Следовательно, AB = NB.
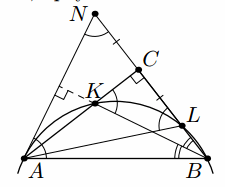
Решение 2: Опустим из точки K перпендикуляр KH на гипотенузу AB (рис. справа). Прямоугольные треугольники KCB и KHB равны по гипотенузе и острому углу. Значит, CB = HB и KC = KH. В описанной окружности четырёхугольника AKLB на хорды AK и KL опираются равные углы, поэтому AK = KL. Значит, прямоугольные треугольники KHA и KCL равны по катету и гипотенузе, откуда HA = CL. Итак, CB + CL = HB + HA = AB.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь