Задача
В центре прямоугольного биллиардного стола длиной 3 м и шириной 1 м стоит биллиардный шарик. По нему ударяют кием в случайном направлении. После удара шар останавливается, пройдя ровно 2 м. Найдите ожидаемое число отражений от бортиков стола.
Решение
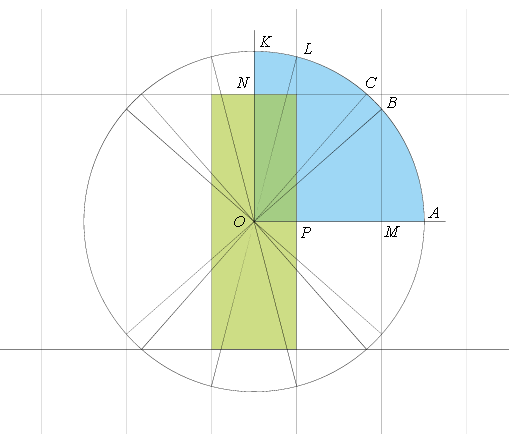
Изобразим сетку с ячейкой 3 м × 1 м. Центральная ячейка сетки – стол, выделенный на рисунке светло-зелёным цветом. Нам потребуется распространить сетку во все стороны настолько, чтобы в нее уместился круг радиусом 2 м с центром в центре стола O.
Позволим шарику "проходить сквозь бортики", катясь прямолинейно по сетке. Отражение от бортика стола соответствует пересечению одной линии сетки. Очевидно можно рассмотреть только четверть круга, то есть все направления, приводящие шар в одну из точек дуги AK.
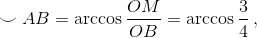
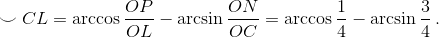Значит, вероятность p2 двух пересечений равна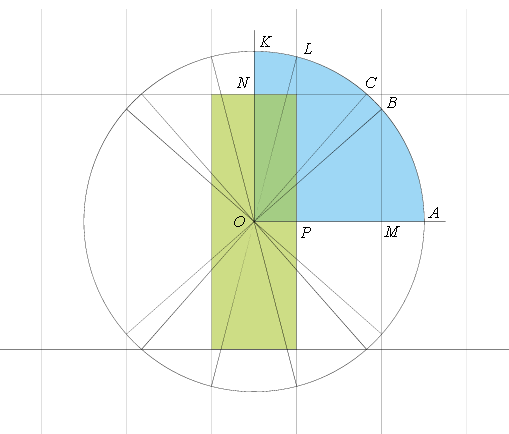 
Вероятность p1 одного пересечения равна 1 – p2. Ожидание числа пересечений p1+ 2p2= 1 +p2=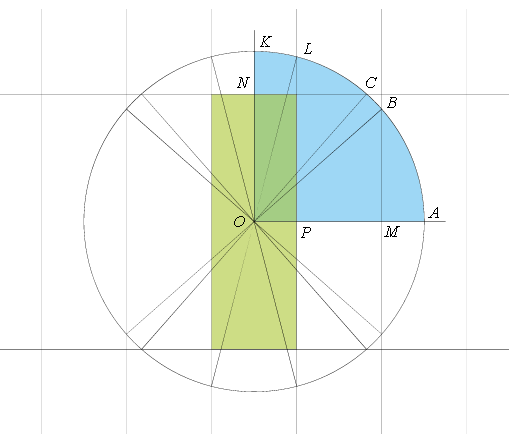 
Ответ
Чтобы оставлять комментарии, войдите или зарегистрируйтесь