Задача
Через вершины B и C треугольника ABC провели перпендикулярно прямой BC прямые b и c соответственно. Серединные перпендикуляры к сторонам AC и AB пересекают прямые b и c в точках P и Q соответственно. Докажите, что прямая PQ перпендикулярна медиане AM треугольника ABC.
Решение
Решение 1: Пусть M – середина стороны BC. Достаточно доказать, что AP² – AQ² = MP² – MQ² (см. задачу 153602).
Поскольку P и Q лежат на серединных перпендикулярах к AC и BC соответственно,
AP² – AQ² = CP² – BQ² = (BC² + BP²) – (BC² + CQ²) = (MB² + BP²) – (MC² + CQ²) = MP² – MQ².
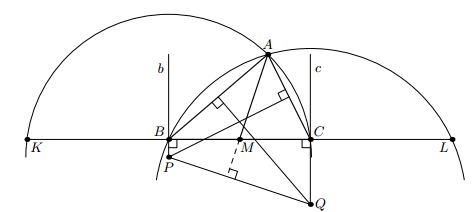
Решение 2: Проведём окружность с центром P, проходящую через A. Она пересечёт прямую BC в точке C и точке K, симметричной C относительно B. Аналогично окружность с центром Q, проходящая через A, пересечёт BC в точке B и точке L, симметричной B относительно C. Степени точки M относительно этих окружностей равны (MC·MK = 3MC² = MB·ML), так что их радикальная ось – это AM и она перпендикулярна линии центров PQ (см. рис.).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь