Задача
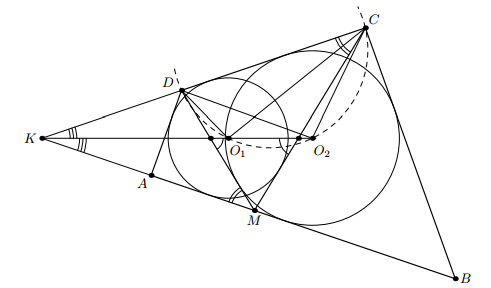
На стороне AB четырёхугольника ABCD нашлась такая точка M, что четырёхугольники AMCD и BMDC описаны около окружностей с центрами O1 и O2 соответственно. Прямая O1O2 отсекает от угла CMD равнобедренный треугольник с вершиной M. Докажите, что четырёхугольник ABCD вписанный.
Решение
Если прямые AB и CD параллельны, то окружности, вписанные в четырёхугольники AMCD и BMDC, равны. Тогда из условия следует, что картинка симметрична относительно перпендикуляра, опущенного из точки M на O1O2, а значит, ABCD – равнобокая трапеция (или прямоугольник).
Пусть прямые AB и CD пересекаются в точке K; без ограничения общности A лежит между K и B. Точки O1 и O2 лежат на биссектрисе угла BKC. По условию прямые CM и DM образуют с этой биссектрисой равные углы; отсюда следует, что ∠DMK = ∠KCM (см. рис.). Поскольку O1 и O2 – центры вписанной в треугольник KMC и вневписанной в треугольник KDM окружностей соответственно, то ∠DO2K = ½ ∠DMK = ½ ∠KCM = ∠DCO1; это значит, что четырёхугольник CDO1O2 вписан. Те же окружности являются вневписанной в треугольник AKD и вписанной в треугольник KBC соответственно, поэтому ∠KAD = 2∠KO1D = 2∠DCO2 = ∠KCB, откуда и следует вписанность четырёхугольника ABCD.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь