Математическая задача о 100 кругов на плоскости

  Пусть K – наименьший из данных кругов (будем считать, что его радиус равен 1), O – центр K, A₁A₂A₃A₄A₅A₆ – правильный шестиугольник с центром O и стороной 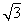. Докажем, что каждый из данных кругов содержит одну из точек O, A₁, ..., A₆; из этого (по принципу Дирихле) будет следовать утверждение задачи.

  Пусть O' – центр некоторого круга K'. Если O' лежит в K, то круг K' содержит O, так как его радиус не меньше 1.

  Разберём случай  OO' > 1.  Луч OO' образует с одним из лучей OA_i угол, не больший 30°. Пусть это луч OA₁, тогда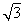  

  Если  1 < O'O ≤ 2,  то  O'A₁ ≤ 1  и K' содержит A₁. Если же  O'O > 2,  то  O'A₁ < O'O – 1.  Но радиус K' не меньше чем  O'O – 1,  так как этот круг пересекается с K; следовательно, и в этом случае K' содержит A₁.

Ответ задачи отсутствует