Задача
Дан фиксированный треугольник ABC. По его описанной окружности движется точка P так, что хорды BC и AP пересекаются. Прямая AP разрезает треугольник BPC на два меньших, центры вписанных окружностей которых обозначим через I1 и I2 соответственно. Прямая I1I2 пересекает прямую BC в точке Z. Докажите, что все прямые ZP проходят через фиксированную точку.
Решение
Решение 1: Как известно, для любых двух окружностей их центры вместе с центрами внутренней и внешней гомотетий, переводящих одну окружность в другую, образуют гармоническую четверку. Для данных окружностей с центрами I1 и I2, центром внешней гомотетии является точка Z, а центр внутренней лежит на прямой AP (поскольку BZ и AP являются общими внешней и внутренней касательными к окружностям). При проекции прямой I1I2 из точки P на описанную окружность Ω треугольника ABC, центр внутренней гомотетии переходит в A, а точки I1 и I2 – в середины дуг AB и AC соответственно. Так как эти три проекции фиксированы, проекция точки Z также не зависит от P. Значит, все возможные прямые ZP проходят через фиксированную точку окружности Ω.
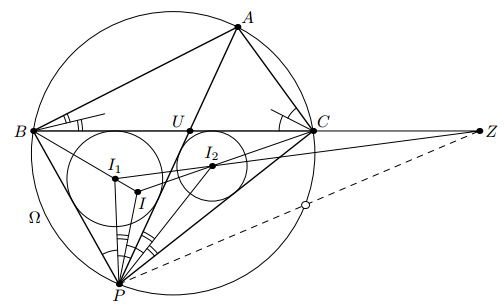
Решение 2: Пусть U – точка пересечения AP и BC. Докажем, что двойное отношение (BCZU) не зависит от P; отсюда проектированием прямой BC на описанную окружность Ω треугольника ABC получается, что прямая PZ пересекает окружность в фиксированной точке.
Пусть I – центр вписанной окружности треугольника PBC соответственно (см. рис.). Применяя теорему Менелая к треугольнику BIC, получаем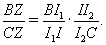 
Поскольку PI, PI1 и PI2 – биссектрисы углов BPC, BPU и UPC соответственно, ∠BPI1 = ∠IPI2 = ½ ∠C и ∠I1PI = ∠I2PC = ½ ∠B. Применяя теорему синусов к треугольникам BPI1, I1PI, IPI2 и I2PC, получаем
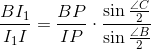и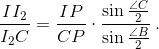 
Применяя теорему синусов к треугольникам BPC, ABU и ACU, имеем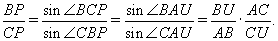 
Перемножая четыре полученных равенства, получаем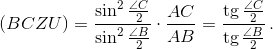 
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь