Задача
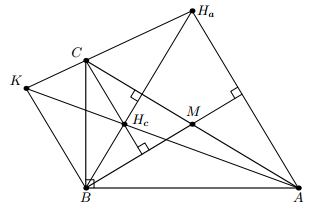
В прямоугольном неравнобедренном треугольнике ABC точка M – середина гипотенузы AC, точки Ha, Hc – ортоцентры треугольников ABM, CBM соответственно, прямые AHc, CHa пересекаются в точке K. Докажите, что ∠MBK = 90°.
Решение
Так как прямые AHa и CHc перпендикулярны BM, четырёхугольник AHaCHc – трапеция, а K – точка пересечения продолжений ее боковых сторон. Кроме того, так как треугольники AMB и CMB равнобедренные, то HaA = HaB и HcC = HcB. Следовательно, KC : KHa = CHc : AHa = BHc : BHa, то есть KB || CHc ⊥ BM (см. рис.).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет