Задача
Можно ли разрезать какой-нибудь прямоугольник на правильный шестиугольник со стороной 1 и несколько равных прямоугольных треугольников с катетами 1 и 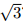 ?
?
Решение
Предположим, что это возможно. Заметим, что площадь S каждого треугольника разбиения равна 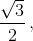 а площадь шестиугольника равна 3S. Каждая сторона прямоугольника разбивается на отрезки длины 1, 2 и
а площадь шестиугольника равна 3S. Каждая сторона прямоугольника разбивается на отрезки длины 1, 2 и
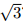 , то есть эти стороны равны
, то есть эти стороны равны 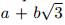 и
и 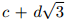 при целых неотрицательных a, b, c, d. Значит, площадь прямоугольника равна
при целых неотрицательных a, b, c, d. Значит, площадь прямоугольника равна 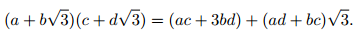
С другой стороны, эта площадь кратна S, что возможно лишь при ac + 3bd = 0, откуда ac = bd = 0. Отсюда следует, что одна сторона прямоугольника (скажем, вертикальная) – целая, а другая (горизонтальная) – целое кратное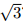 . Значит, его площадь кратна 2S. Поскольку площадь шестиугольника равна 3S, число треугольников в разбиениинечётно.
Каждый (непродолжаемый) отрезок разбиения, лежащий внутри прямоугольника, покрыт отрезками целых длин и отрезками длины
. Значит, его площадь кратна 2S. Поскольку площадь шестиугольника равна 3S, число треугольников в разбиениинечётно.
Каждый (непродолжаемый) отрезок разбиения, лежащий внутри прямоугольника, покрыт отрезками целых длин и отрезками длины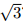 с обеих сторон. Поскольку представление его длины в виде
с обеих сторон. Поскольку представление его длины в виде  единственно, к нему примыкает чётное число отрезков длины
единственно, к нему примыкает чётное число отрезков длины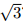 .
К вертикальным сторонам прямоугольника таких отрезков не прилегает, а горизонтальные стороны из них состоят, так что к горизонтальным сторонам
таких отрезков прилегает поровну. Значит, общее число таких отрезковчётно, а в каждом треугольнике ровно по одному такому отрезку. Противоречие.
.
К вертикальным сторонам прямоугольника таких отрезков не прилегает, а горизонтальные стороны из них состоят, так что к горизонтальным сторонам
таких отрезков прилегает поровну. Значит, общее число таких отрезковчётно, а в каждом треугольнике ровно по одному такому отрезку. Противоречие.
Ответ
Нельзя.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь