Задача
В треугольнике ABC медианы AA0, BB0, CC0 пересекаются в точке M.
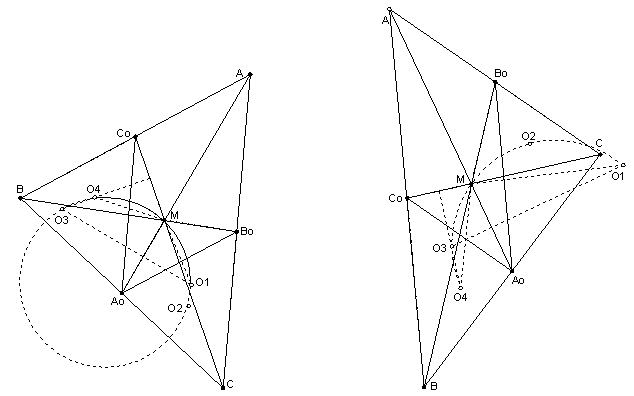
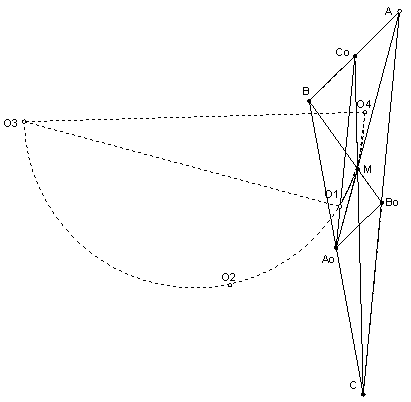
Докажите, что центры описанных окружностей треугольников MA0B0, MCB0, MA0C0, MBC0 и точка M лежат на одной окружности.
Решение
Пусть ω1, ω2, ω3, ω4 – указанные в условии окружности (в порядке их перечисления), а O1, O2, O3, O4 – их центры. Чтобы избежать разбора случаев, считаем все углы ориентированными. Так как невыпуклый четырёхугольник MB0A0C0 не может быть вписанным, то точки O1 и O3 различны. Прямая O1O3 – серединный перпендикуляр к MA0, поэтому MO1O3 – треугольник с описанной окружностью ω.
Угол MO1O3 равен половине центрального угла MO1A0 окружности ω1, то есть вписанному в неё углу MB0A0. Если O4 совпадает с O3, то всё доказано, иначе прямая O4O3 – серединный перпендикуляр к отрезку MС0, поэтому угол MO4O3 равен половине центрального угла MO4C0 окружности ω4, то есть вписанному в неё углу MBC0. А углы MB0A0 и MBС0 равны из параллельности B0A0 и BС0. Поэтому ∠MO1O3 = ∠MO4O3, то есть O4 лежит на ω. Аналогично O2 лежит на ω.
На рисунках приведены различные случаи расположения точек.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь