Задача
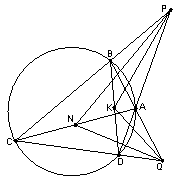
Дан вписанный четырёхугольник АВСD. Продолжения его противоположных сторон пересекаются в точках P и Q. Пусть К и N – середины диагоналей.
Докажите, что сумма углов PKQ и PNQ равна 180°.
Решение
Обозначим точки как на рисунке. Треугольники ACP и BDP подобны, поскольку у них углы C и D опираются на одну дугу, а угол P общий. Поэтому соответственные медианы в них отсекают подобные треугольники ANP и BKP. Значит, углы ANP и BKP равны. Аналогично подобие треугольников ACQ и DBQ влечёт равенство углов ANQ и DKQ. Следовательно, ∠PKQ + ∠PNQ = ∠PKQ + ∠BKP + ∠DKQ = ∠BKD = 180°.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет