Задача
Окружность с центром I лежит внутри окружности с центром O. Найдите геометрическое место центров описанных окружностей треугольников IAB, где AB – хорда большей окружности, касающаяся меньшей.
Решение
Пусть R – радиус большей, a r – радиус меньшей из данных окружностей, d = OI, K – точка касания хорды AB с меньшей окружностью.
Если M – такая точка, что OM ⊥ AB, то OM и IK параллельны и
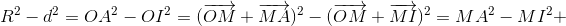
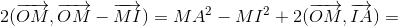
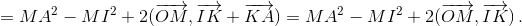
Пусть M – центр описанной окружности треугольника IAB. Тогда прямая OM – серединный перпендикуляр к AB, поэтому выполнено вышеприведённое равенство. А так как MA = MI, то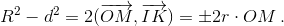 
Знака минус, однако, быть не может, так как R > d, поэтому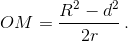 
Обратно, пусть M – такая точка, что 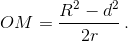Рассмотрим хорду AB большей окружности, касающуюся меньшей в такой точке K, что 
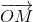и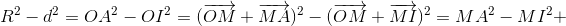 
сонаправлены. Тогда M лежит на диаметре, перпендикулярном к хорде AB, и поэтому MA = MB. Кроме того, выполнено приведённое выше равенство, причём 
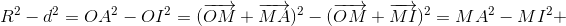Подставив туда значение OM, получим MA² – MI² = 0, то есть MI = MA = MB. Следовательно, M – центр описанной окружности треугольника IAB.
Ответ
Окружность с центром O и радиусом R²–OI²/2r, где R и r – радиусы данных окружностей.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь