Отношение сторон прямоугольника с ломаной — задача Стрелковой
Задача
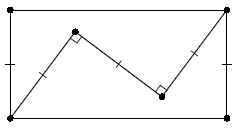
В прямоугольнике проведена ломаная, соседние звенья которой перпендикулярны и равны меньшей стороне прямоугольника (см. рис).
Найдите отношение сторон прямоугольника.
Решение
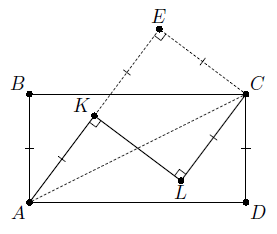
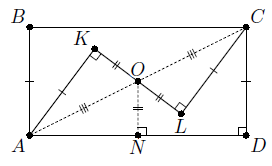
Пусть нам дан прямоугольник ABCD и ломаная AKLC. Первый способ. Достроим прямоугольный равнобедренный треугольник KLC до квадрата KECL (рис. слева). Точки A, K и E лежат на одной прямой. Следовательно, прямоугольные треугольники AEC и ADC равны по гипотенузе и катету. Поэтому AD = AE = 2AK = 2AB.
Ответ
1 : 2.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет