Задача
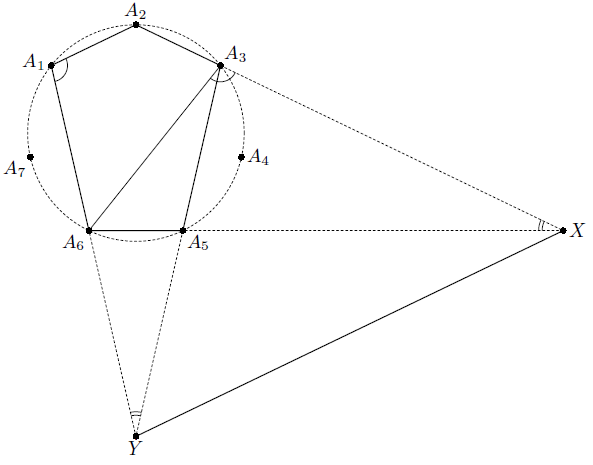
Дан правильный семиугольник A1A2A3A4A5A6A7. Прямые A2A3 и A5A6 пересекаются в точке X, а прямые A3A5 и A1A6 – в точке Y.
Докажите, что прямые A1A2 и XY параллельны.
Решение
Докажем, что ∠A2A1Y + ∠XYA1 = 180°, откуда и будет следовать утверждение задачи. Рассмотрим описанную окружность данного семиугольника (см. рис.). Поскольку четырёхугольник A1A2A3A6 – вписанный, то ∠A2A1A6 = ∠XA3A6. Теперь достаточно доказать, что четырёхугольник XA3A6Y вписанный.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет