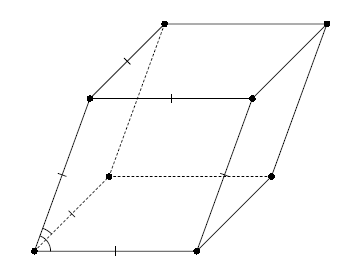
При  n = 4  призма может быть и наклонной. Достаточно рассмотреть, например, четырёхугольную призму, у которой все грани – равные ромбы (такая фигура называется ромбоидом, рис. слева).

  Теперь докажем, что в остальных случаях  (n= 3  и  n> 4)  призма обязательно будет прямой.   Пусть это не так, то есть боковые грани призмы – равные параллелограммы, не являющиеся прямоугольниками. Тогда вершины основания являются вершинами трёхгранных углов двух типов:   1) с двумя равными плоскими углами;   2) с двумя плоскими углами, в сумме дающими 180°.   В первом случае проекция общего ребра для этих углов принадлежит прямой, содержащей биссектрису внутреннего угла многоугольника в основании, а во втором – внешнего.   Заметим, что соседние вершины основания – разных типов. Действительно, поскольку проекции параллельных прямых параллельны, то, в противном случае, мы получим параллельность биссектрис двух соседних внутренних или внешних углов выпуклого многоугольника, что невозможно.   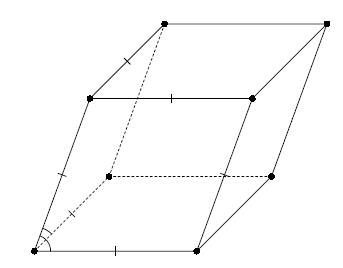Рассмотрим любые три последовательные грани:AA₁D₁D,AA₁B₁BиBB₁C₁C. ПустьA'иB'– проекцииA₁иB₁соответственно на плоскость основания призмы, причёмA'принадлежит прямой, содержащей биссектрису внутреннего углаDABмногоугольника в основании, аB'– внешнего углаCBK(рис. справа). Тогда прямыеAA'иBB'параллельны, то есть  ∠A'AK= ∠B'BK,  откуда  ∠DAB= ∠CBK,  следовательно, прямые AD иBCпараллельны.   Итак, мы доказали, что у многоугольника в основании призмы стороны через одну параллельны. Учитывая его выпуклость, получим, что он является параллелограммом. Противоречие.

При всех  n ≠ 4.