Задачи и олимпиады по математике

Задача

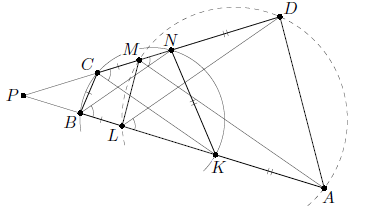
На стороне AB выпуклого четырёхугольника ABCD взяты точки K и L (точкаK лежит между A и L), а на стороне CD взяты точки M и N (точка M между C и N). Известно, что AK = KN = DN и BL = BC = CM. Докажите, что если BCNK – вписанный четырёхугольник, то и ADML тоже вписан.

Решение

В случае AB || CD имеем BC = KN, поэтому AK = BL = CM = DN. Значит, четырёхугольник LMDA получается из BCNK параллельным переносом на вектор BL.

Пусть теперьABиCDне параллельны; обозначим черезPточку пересечения прямыхABиCD. Так как четырёхугольникBCNKвписан, треугольникиPBCиPNKподобны; отсюда PB:BL = PB:BC = PN:NK = PN:ND. Значит, BN || LD. Аналогично CK || MA. Отсюда ∠ALD= ∠KBN и ∠KCN= ∠AMD. Так как четырёхугольникBCNKвписан, то ∠KBN= ∠KCN. Поэтому и ∠ALD= ∠AMD, то естьADMLтакже вписан.

Ответ

Ответ задачи отсутствует

Задача

Решение

Ответ

Подтверждение удаления