Задача
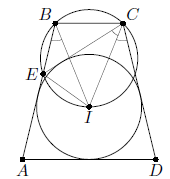
Внутри равнобокой трапеции ABCD с основаниями BC и AD расположена окружность ω с центром I, касающаяся отрезков AB, CD и DA. Описанная окружность треугольника BIC вторично пересекает сторону AB в точке E. Докажите, что прямая CE касается окружности ω.
Решение
Заметим, что точка I лежит на оси симметрии трапеции. Пользуясь этим, а также вписанностью четырёхугольника CBEI, получаем
∠ICD = ∠IBA = ∠IBE = ∠ICE. Так как прямая CD касается окружности ω, то и прямая CE, симметричная ей относительно CI, также касается ω.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет