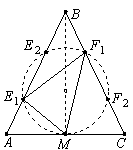
Рассмотрим описанную окружность треугольника MEF. Угол между касательной и хордой MF равен  ∠MEF = ∠FMC.  Поэтому MC и есть касательная. Значит, центр окружности лежит на высоте BM. Следовательно, эта высота является осью симметрии рисунка. Поскольку  AE ≠ CF,  то окружность пересекает каждую из боковых сторон в двух точках. Причём E и F не симметричны. Два возможных случая снабжены соответствующими индексами (см. рис.). Рассмотрим их.

  1) Внешний уголAE₁Mвписанного четырёхугольникаME₁E₂F₂равен углуMF₂E₂, а последний равен симметричному углу  ME₁F₁, равному α.   2) Вписанные углыAE₂MиME₂F₂, равный α опираются на симметричные дуги.

α.