Задача
В четырёхугольнике ABCD AB = CD, M и K – середины BC и AD. Докажите, что угол между MK и AC равен полусумме углов BAC и DCA.
Решение
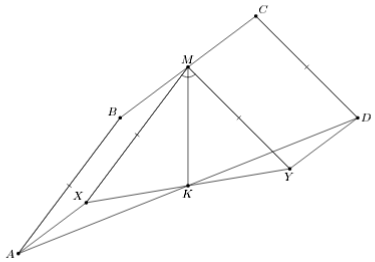
Построим параллелограммы ABMX и DCMY (см. рис.). Так как AX = BM = MC = DY и AX || BC || DY, то AXDY тоже параллелограмм, а K – его центр. Кроме того, MX = AB = CD = MY, следовательно, MK – медиана, а значит, и биссектриса равнобедренного треугольника XMY, что равносильно утверждению задачи.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет