Назад
Задача 165805 • Сложность: 3 • 9-10 класс
Задача

На стороне BC треугольника ABC взята произвольная точка D. Через D и A проведены окружности ω1 и ω2 так, что прямая BA касается ω1, прямая CA касается ω2. BX – вторая касательная, проведённая из точки B к окружности ω1, CY – вторая касательная, проведённая из точки C к окружности ω2. Докажите, что описанная окружность треугольника XDY касается прямой BC.

Авторы:
Хилько Д.
Разделы:
Планиметрия
Источники:
Олимпиады и турниры Олимпиада по геометрии имени И.Ф. Шарыгина XII Олимпиада по геометрии имени И.Ф. Шарыгина (2016 г.)
Количество версий:
4
Решение

  Сделаем инверсию относительно окружности произвольного радиуса с центром в точке D. Образы точек будем обозначать штрихами (см. рис.).

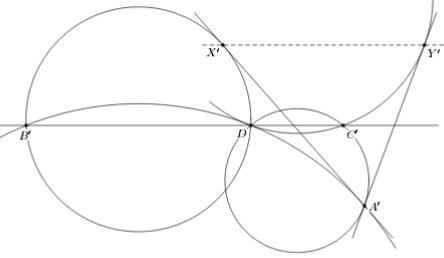
  Описанная окружность ω1треугольникаXDAкасаласьBAиBX, значит, она перейдёт в прямуюA'X', а указанные прямые прямые – в описанные окружности треугольниковB'DA'иB'DX', причём они будут касаться прямойX'A'. Поэтому радикальная осьB'Dэтой пары окружностей делит пополам отрезокX'A'. Аналогично радикальная осьDC'описанных окружностей треугольниковDC'Y'иDC'A'делит пополам отрезокA'Y'. Значит, прямаяB'C'– средняя линия треугольникаX'A'Y', откуда  X'Y' || B'C'.  Остаётся заметить, что прообраз прямойX'Y'– описанная окружность треугольникаXYD. Так как  X'Y' || B'C',  она касается прямойBCв точкеD.
Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет