Задачи и олимпиады по математике

Задача

В клетках первого столбца таблицы n&timesn записаны единицы, в клетках второго – двойки, ..., в клетках n-го – числа n. Числа на диагонали, соединяющей левое верхнее число с правым нижним, стёрли. Докажите, что суммы чисел по разные стороны от этой диагонали отличаются ровно в два раза.

Решение

Решение 1: Сумма чисел в k-й строке под диагональю равна 1 + 2 + ... + (k – 1) = ½ k(k – 1). Сумма чисел в k-м столбце над диагональю вдвое больше: она равна (k – 1)k. Поэтому и сумма всех чисел над диагональю вдвое больше суммы под диагональю.

Решение 2: Рассмотрим еще две таблицы:

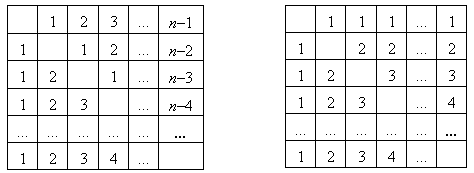
В обеих равны суммы по разные стороны от пустой диагонали (наборы чисел в столбцах под диагональю совпадают с наборами в строках над диагональю в правой таблице и наборами в диагоналях, параллельных пустой, – в левой). Заметим теперь, что если сложить попарно числа из соответствующих клеток над диагональю разных таблиц, получим таблицу из условия задачи.

Ответ

Ответ задачи отсутствует

Задача

Решение

Ответ

Подтверждение удаления