Муравей и рёбра додекаэдра: задача по олимпиадной математике

Решение 1:   Предположим, что это не так. Тогда на каждом перекрёстке все три раза муравей поворачивает либо только налево, либо только направо. Расположим произвольно левые и правые перекрестки в вершинах додекаэдра и рассмотрим соответствующие маршруты муравья. Получим набор циклов. При замене "знака" одного из перекрёстков происходит перестройка: если к перекрёстку подходит три цикла, они склеиваются в один, если два – они переклеиваются в два другие, если один – остаётся один или он распадается на три (см. рисунки).

  В любом случае,чётностьколичества циклов сохраняется. Если все перекрёстки левые, то будет 12 циклов (соответствующих граням додекаэдра). Значит, один цикл никогда не получится.

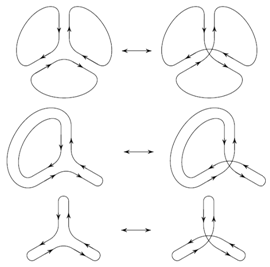
Решение 2:

  Докажем равносильное утверждение: если все рёбра пройдены муравьём в обоих направлениях, то в какой-то вершине муравей повернул назад.

  Зададим две перестановки на множестве направленных рёбер додекаэдра: p переводит каждое ребро в следующее на маршруте, а t меняет на каждом ребре направление на противоположное. Заметим, что если ребро e входит в некоторую вершину v, то p(e) выходит из неё, а t(p(e)) снова входит в v. Обозначим через s_v перестановку, выполняемую tp на множестве рёбер, входящих в v. Тогда tp распадается в произведение 20 перестановок s_v – по одной для каждой вершины додекаэдра. Перестановка p – цикл длины 60 – нечётна, а t – произведение 30 транспозиций – чётна. Поэтому перестановка tp нечётна, а значит, хотя бы одна из перестановок s_v нечётна. Нечётная перестановка трёх рёбер может либо оставлять все рёбра на месте, либо переставлять два ребра, а третье оставлять на месте. Вот на этом-то третьем ребре муравей и повернул вспять!

Ответ задачи отсутствует