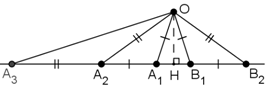
Пусть l – данная прямая, O – отмеченная точка вне её, ОH – перпендикуляр, опущенный на l.

  Оценка. Основание равнобедренного треугольника может лежать на l или не лежать. Рассматриваемые треугольники первого вида симметричны относительно OH, поэтому их не больше 50 – половины отмеченных точек на l. Треугольников второго вида с данным основанием OA может быть не более одного, так как вершина определяется пересечением l и серединного перпендикуляра к OA. Поэтому треугольников второго вида не больше 100.

  Пример 1. Отложим от луча OH лучи под углом 18°. Они пересекут l в точках A₁ и B₁, отметим их. Отложим на l в другую сторону от A₁B₁ отрезок

A₁A₂ = A₁O,  затем отрезок  A₂A₃ = A₂O,  ..., отрезок  A₄₉A₅₀ = A₄₉O.  Аналогично отметим точки B₂, ..., B₅₀. Равнобедренными будут 50 треугольников OA_iB_i, по 49 треугольников OA_iA_i+1 и OB_iB_i+1, треугольники OA₁B₂ и OB₁A₂ с углами 72°, 72°, 36°.

 Пример2. Рассмотрим вершины правильного 101-угольника. Отметим одну из них –O, её соседей –AиB, а для каждой из остальных вершинXотметим её образX'при инверсии с центромOи радиусомOA. Тогда все отмеченные точки, кромеO, лежат наAB(причём лучи, идущие в них, разбивают уголAOBна 99 равных углов). Так как при инверсии треугольникиOXYиOY'X'подобны, то количество равнобедренных треугольников с вершинами в отмеченных точках равно количеству равнобедренных треугольников видаOXY, гдеXиY– вершины 101-угольника. А таких треугольников – 50 с основанием, не содержащимO, и 100 с основанием, содержащимO.

150 треугольников.