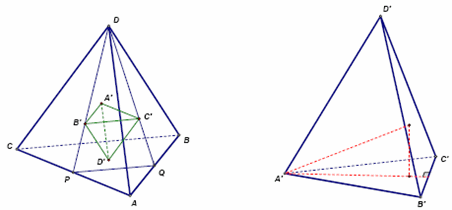
Пусть АВСD – данный тетраэдр, A', B', C', D' – точки пересечения медиан граней BCD, CDA, DAB, ABC. Грани тетраэдра A', B', C', D' параллельны соответственным граням исходного тетраэдра. Так, например, плоскость ABC параллельна плоскости A'B'C' и т.д.

  Действительно, пусть точкиPиQ– середины рёберАСиАВ. Так как точка пересечения делит медианы в отношении  2 : 1,  то по обратной теореме Фалеса  B'С' || PQ.  Но  PQ || BC  как средняя линия, следовательно,  B'С' || BC.  Точно так же  A'С' || AC,  и по признаку параллельности двух плоскостей грани параллельны.   Поэтому перпендикуляры, восстановленные из точекA', B', C', D'  к соответствующим гранямАВСD, являются высотами тетраэдраA'B'C'D'.   По теореме о трёх перпендикулярах их проекции на плоскость грани являются высотами этой грани и, значит, пересекаются в одной точке. Следовательно, их проекции на параллельную плоскостьАВСтакже пересекаются в одной точке.

Ответ задачи отсутствует