Назад
Задача 166015 • Сложность: 3 • 9-11 класс
Задача

Равносторонний треугольник ABC вписан в окружность Ω и описан вокруг окружности ω. На сторонах AC и AB выбраны точки P и Q соответственно так, что отрезок PQ касается ω. Окружность Ωb с центром P проходит через вершину B, а окружность Ωc с центром Q – через C. Докажите, что окружности Ω, Ωb и Ωc имеют общую точку.

Авторы:
Акопян А. В. Кожевников П. А.
Разделы:
Планиметрия
Источники:
Олимпиады и турниры Всероссийская олимпиада по математике 2016-2017 Региональный этап
Количество версий:
4
Решение

  Обозначим через O центр треугольника ABC.   Первый способ. Пусть Ω касается отрезков BQ, QP и PC в точках K, L и M соответственно (рис. слева). В силу симметрии равностороннего треугольника прямые BO и CO проходят через точки M и K соответственно.

  Отложим на луче LO отрезок  OX = OA  (так что X лежит на окружности Ω). Отрезки LX и MB симметричны относительно прямой PO, значит,

PX = PB,  то есть точка X лежит на окружности Ωb. Аналогично X лежит и на окружности Ωc.

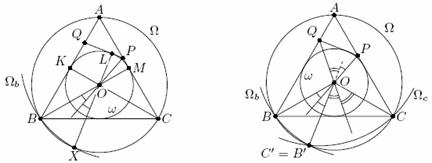
  Второй способ. Окружности Ω и Ωb пересекаются в точке B. Вторая точка B' их пересечения симметрична точке B относительно линии центров PO (рис. справа). Аналогично вторая точка C' пересечения окружностей Ω и Ωc симметрична точке C относительно QO.

  Докажем, что точки B' и C' совпадают. Поскольку  OB' = OB = OC = OC';  достаточно проверить, что  ∠BOB' + ∠COC' = ∠BOC (= 120°).  Поскольку прямые PO и QO – биссектрисы углов BOB' и COC', последнее равенство равносильно равенству  ∠POQ = 60°.

  Но  ∠POQ = 180° – ½ (∠BQP + ∠CPQ) = 180° – ½ (360° – ∠B – ∠C) = 60°.

Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет