Задача
Изначально на доске записаны несколько натуральных чисел (больше одного). Затем каждую минуту на доску дописывается число, равное сумме квадратов всех уже записанных на ней чисел (так, если бы на доске изначально были записаны числа 1, 2, 2, то на первой минуте было бы дописано число 1² + 2² + 2²). Докажите, что сотое дописанное число имеет хотя бы 100 различных простых делителей.
Решение
Пусть S1, ..., S100 – числа, которые были записаны на доске в первые 100 минут. Пусть перед дописыванием числа Si на доске были числа a1, ..., ak. Тогда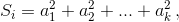 
а следующее дописанное число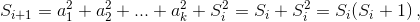 
Значит, Si+1 содержит в своем разложении на простые множители все простые числа, на которые делится Si. Кроме того, поскольку Si и Si + 1 взаимно просты, Si+1 содержит хотя бы один новый простой множитель (делитель числа Si + 1). Так как S1 > 1, то S1 содержит в своем разложении хотя бы один простой множитель. Отсюда последовательно получаем, что для i = 1, 2, ..., 100 число Si содержит в своем разложении хотя бы i различных простых множителей.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь