Задача
Четырёхугольник ABCD вписан в окружность Г c центром в точке O. Его диагонали AC и BD перпендикулярны и пересекаются в точке P, причём точка O лежит внутри треугольника BPC. На отрезке BO выбрана точка H так, что ∠BHP = 90°. Описанная окружность ω треугольника PHD вторично пересекает отрезок PC в точке Q. Докажите, что AP = CQ.
Решение
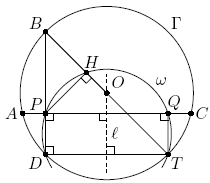
Проведём в окружности Г диаметр BT (см. рис.). Точки H и D лежат на окружности с диаметром PT, значит, она совпадает с ω. Поэтому
∠PQT = ∠PHT = 90°, то есть PQTD – прямоугольник.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет