Пересчет оценок: задача по олимпиадной математике
Задача
Преподаватель выставил оценки по шкале от 0 до 100. В учебной части могут менять верхнюю границу шкалы на любое другое натуральное число, пересчитывая оценки пропорционально и округляя до целых. Нецелое число при округлении меняется до ближайшего целого; если дробная часть равна 0,5, направление округления учебная часть может выбирать любое, отдельно для каждой оценки. (Например, оценка 37 по шкале 100 после пересчета в шкалу 40 перейдёт в 37·40/100 = 14,8 и будет округлена до 15.)
Студенты Петя и Вася получили оценки a и b, отличные от 0 и 100. Докажите, что учебная часть может сделать несколько пересчётов так, чтобы у Пети стала оценка b, а у Васи – оценка a (пересчитываются одновременно обе оценки).
Решение
Оценку "a баллов из n возможных" будем обозначать кратко a/n. Оценки 0/n и n/n будем называть крайними. Лемма 1. Если последовательно менять шкалы в порядке 100 → 99 → 98 → 97 → ... → 3 → 2, то любая некрайняя оценка a/100 превратится в 1/2.
Доказательство. Достаточно заметить, что при этих заменах шкал некрайние оценки остаются некрайними, так как при всех k > 1 оценка 1/k ближе к любой некрайней оценке вида a/(k+1), чем 0/k; значит, на очередном шаге после округления оценка 0/k (аналогично k/k) не могла получиться. Таким образом, в конце останется некоторая некрайняя оценка в двухбалльной шкале, то есть 1/2. Лемма 2. Дано натуральное число k. Если менять шкалы в порядке 2 → 3 → 4 → 6 → 8 → ... → 2·2s → 3·2s → 2·2s+1 → ... → 2k, то можно получить из исходной оценки 1/2 любую оценку вида (2r+1)/2k, где 0 ≤ r < 2k–1.
Доказательство. Будем вести индукцию по k.
База (k = 1). Никаких операций не произошло, начальное состояние 1/2.
Шаг индукции. Рассмотрим случай, когда r нечётно. По предположению индукции за первые 2(k – 2) замен шкал можно получить оценку r/2k–1. Выясним, что произойдёт при переходе в следующую шкалу (2k–1 → 3·2k–2). 3·2k–2 = 3/2·2k–1, поэтому оценка r перейдёт в 3r/2. Это полуцелое число округлим до 3r+1/2. При переводе в финальную шкалу (3·2k–2 → 2k) оценка 3r+1/2 перейдёт в 4/3·3r+1/2 = 2r + 2/3, что округляется до 2r + 1.
Случай чётного r разбирается аналогично, при этом возникает следующая последовательность оценок: r + 1 → 3r/2 + 1 → 2r + 1.
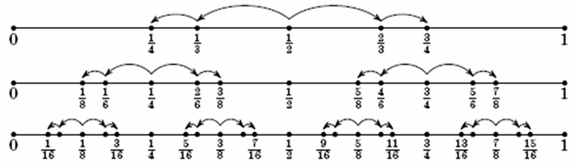
Каждая следующая пара шагов содержит две копии предыдущей пары, сжатые в два раза.
Доказательство. От противного: пусть некоторая оценка a/100 не получается таким действием. Тогда в интервале (a/100 – 1/200, a/100 + 1/200) нет дробей вида 2r+1/256. Но длина этого интервала равна 1/100, а расстояние между соседними дробями такого вида равно 1/128. Противоречие. Теперь решим задачу. В начале по алгоритму из леммы 1 приведём обе оценки к состоянию 1/2. Затем, действуя согласно лемме 2, получим из двух экземпляров 1/2 любую пару нечётных оценок по шкале от 0 до 256. Лемма 3 гарантирует, что при возврате в исходную шкалу от 0 до 100 можно получить любую пару оценок.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь