Задача
На вписанной окружности треугольника ABC, касающейся стороны AC в точке S, нашлась такая точка Q, что середины отрезков AQ и QC также лежат на вписанной окружности. Докажите, что QS – биссектриса угла AQC.
Решение
Решение 1:Пусть K и L – середины отрезков AQ и QC соответственно (cм. рисунок). KL – средняя линия треугольника AQC, поэтому KL || AC. Параллельные прямые KL и AC высекают на вписанной окружности равные дуги KS и SL. Значит, опирающиеся на них углы KQS и SQL равны.
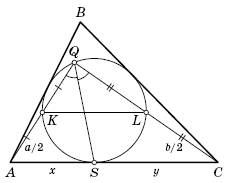
Решение 2:Пусть AQ = u, QC = v, AS = x, SC = y. По теореме о касательной и секущей имеем u²/2 = x², v²/2 = y². Отсюда x : u = y : v, то есть точка S делит сторону AC треугольника AQC на части, пропорциональные прилежащим сторонам. В таком же отношении эту сторону делит и основание биссектрисы угла Q этого треугольника.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь