Задача
Прямая касается окружности в точке A. На прямой выбрали точку B и повернули отрезок AB на некоторый угол вокруг центра окружности, получив отрезок A'B'. Докажите, что прямая, проходящая через точки касания A и A', делит пополам отрезок BB'.
Решение
Решение 1:Докажем, что равны перпендикуляры BD и B'D', опущенные на прямую AA'. Когда AA' – диаметр, это очевидно. Иначе треугольники ABD и AB'D' равны по гипотенузе и острому углу. Поэтому BDB'D' – параллелограмм, и прямая AA', содержащая его диагональ DD', делит другую диагональ пополам.
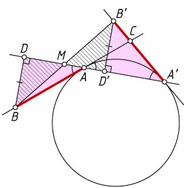
Решение 2:Отложим на прямой AB отрезок AL, равный AB. При симметрии относительно диаметра, перпендикулярного AA', отрезок касательной AL перейдёт в A'B'. Поэтому либо прямая LB' параллельна AA' (но AA' не параллельна LB, и поэтому B' не лежит на прямой LB), либо точки L и B' совпадают. В первом случае прямая AA' содержит среднюю линию треугольника LBB', а значит, проходит через середину стороны BB'. Во втором случае A – середина BB'.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь