Задача
I – центр вписанной окружности треугольника ABC, HB, HC – ортоцентры треугольников ABI и ACI соответственно, K – точка касания вписанной окружности треугольника со стороной BC. Докажите, что точки HB, HC и K лежат на одной прямой.
Решение
Так как прямые BHB и CHC перпендикулярны AI, то BHBCHC – трапеция и её диагонали делят друг друга в отношении BHB : CHC. Поскольку проекции M, N точек HB, HC на AB и AC являются точками касания вписанной окружности с соответствующими сторонами, то
BM = BK, CN = CK. Кроме того, так как ∠HBBM = 90° – ∠A/2 = ∠HCCN, то прямоугольные треугольники HBBM и HCCN подобны. Следовательно, BHB : CHC = BM : CN = BK : CK, то есть точка пересечения диагоналей трапеции совпадает с K (см. рис.).
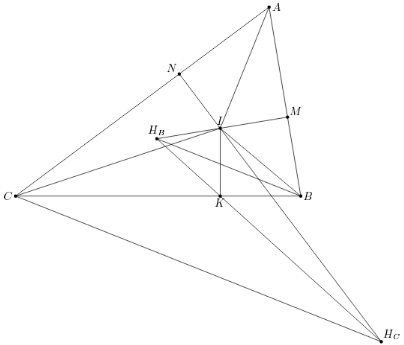
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь