Задача
Дан четырёхугольник ABCD, в котором AC = BD = AD; точки E и F – середины AB и CD соответственно; O – точка пересечения диагоналей четырёхугольника. Докажите, что EF проходит через точки касания вписанной окружности треугольника AOD с его сторонами AO и OD.
Решение
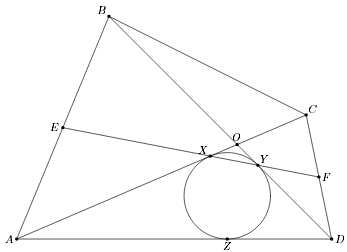
Пусть X, Y, Z – точки касания указанной вписанной окружности со сторонами AO, OD, AD соответственно. Тогда DY = DZ и, значит,
BY = AZ = AX. Кроме того, OX = OY. Применив теорему Менелая к треугольнику AOB и прямой XY, получим, что эта прямая проходит через E. Аналогично она проходит через F (см. рис.).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет