Задача
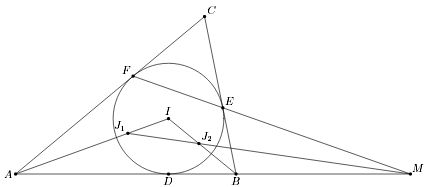
В остроугольный треугольник ABC вписана окружность с центром I, касающаяся сторон AB, BC и CA в точках D, E и F соответственно. В четырёхугольники ADIF и BDIE вписаны окружности с центрами J1 и J2 соответственно. Прямые J1J2 и AB пересекаются в точке M. Докажите. что CD ⊥ IM.
Решение
Так как DJ1 – биссектриса треугольника DIA, то AJ1 : J1I = AD : ID. Аналогично IJ2 : J2B = DI : DB. По теореме Менелая
AF/FC·CE/EB·BM/MA = AD/DB·BM/MA = AJ1/J1I·IJ2/J2B·BM/MA = 1, то есть точка M лежит на прямой FE (см. рис.). Поскольку C и D – полюсы прямых EF и AB относительно вписанной окружности, то M – полюс прямой CD, следовательно, CD ⊥ IM.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет