Углы треугольника ABC с центрами O и H
Задача
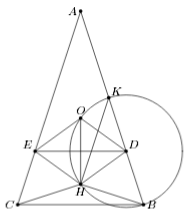
В треугольнике ABC O – центр описанной окружности, H – ортоцентр. Через середину OH параллельно BC проведена прямая, пересекающая стороны AB и AC в точках D и E. Оказалось, что O – центр вписанной окружности треугольника ADE. Найдите углы треугольника ABC.
Решение
Из условия следует, что AO – биссектриса угла A, то есть AB = AC. Значит, ODHE – ромб. Первый способ. ∠ODH = 2∠ODE = ∠B, ∠DOH = ∠DHO = 90° – ∠B/2 = ∠BHD.
Пусть прямая, проходящая через H параллельно AC, пересекает AB в точке K. Так как ∠HKB = ∠A = ∠HOB, точки H, O, K, B лежат на одной окружности. Поскольку угол KHB – прямой, центр этой окружности лежит на прямой AB и, значит, совпадает с точкой D (см. рис.). Следовательно, ∠HBD = ∠BHD = 90° – ∠B/2. С другой стороны, этот угол равен ∠B – ∠A/2, откуда и следует ответ.
Ответ
∠A = 36°, ∠B = ∠C = 72°.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь