Задача
В равнобедренной трапеции ABCD с основаниями BC и AD диагонали AC и BD перпендикулярны. Из точки D опущен перпендикуляр DE на сторону AB, а из точки C – перпендикуляр CF на прямую DE. Докажите, что ∠DBF = ½ ∠FCD.
Решение
EDB = 45° – (90° – ∠A) = ∠A – 45° = ∠BDC. Значит, точка B равноудалена от прямых DE и DC. Поскольку трапеция равнобедренная, расстояние от B до DC равно расстоянию от C до AB, которое, в свою очередь, равно расстоянию от B до параллельной AB прямой CF. Следовательно, BF – биссектриса угла CFE, то есть ∠BFC = 45°. Пусть перпендикуляр к BF, восставленный из точки F, пересекает BD в точке K. Тогда
∠CFK = ∠CBK = 45°, значит, четырёхугольник BFKC вписанный и CK ⊥ BC. Так как CF || AB, то прямая CK является биссектрисой угла FСВ, и ∠DBF = ∠KCF = ½ ∠FCD (см. рис.).
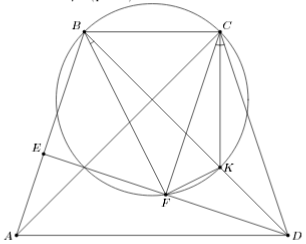
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь