Задача
Дан остроугольный треугольник ABC. Постройте на сторонах BC, CA, AB точки A', B', C' так, чтобы выполнялись следующие условия:
- A'B' || AB;
- C'C – биссектриса угла A'C'B';
- A'C' + B'C' = AB.
Решение
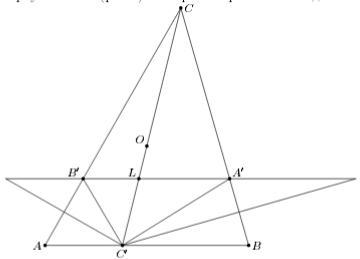
Пусть L – точка пересечения отрезков CC' и A'B'. Тогда BC' : AC' = A'L : B'L = A'C' : B'C' и из равенства A'C' + B'C' = AB получаем, что BC' = C'A', AC' = C'B'. Поэтому точки CA и CB, симметричные C' относительно AC и BC лежат на прямой A'B', а AC'B'CA – ромб.
∠CC'B' = ∠CCACB = ∠CCBCA = ½ (180° – 2∠C) = 90° – ∠C, значит, ∠B'CC' = ∠AB'C – ∠CC'B' = ∠A – (90° – ∠C) = 90° – ∠B, то есть прямая CC' проходит через центр описанной окружности (см. рис.). Теперь построение очевидно.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь