Задача
Четырёхугольник ABCD вписан в окружность ω с центром O, M1 и M2 – середины сторон AB и CD соответственно; Ω – описанная окружность треугольника OM1M2, X1 и X2 – точки пересечения ω с Ω, а Y1 и Y2 – вторые точки пересечения описанных окружностей ω1 и ω2 треугольников CDM1 и ABM2 соответственно с Ω. Докажите, что X1X2 || Y1Y2.
Решение
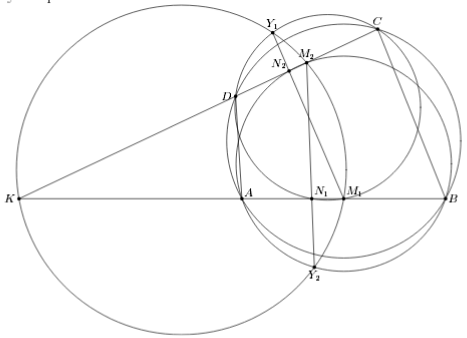
Пусть K – точка пересечения прямых AB и CD. Так как углы OM1K и OM2K прямые, OK – диаметр окружности ω. Поскольку X1X2 ⊥ OK, для решения задачи достаточно доказать, что дуги KY1 и KY2 равны, то есть что ∠KM1Y1 = ∠KM2Y2.
Пусть N1, N2 – вторые точки пересечения окружностей ω1 и ω2 с AB и CD соответственно. Тогда KM1·KN1 = KC·KD = KA·KB, следовательно, N1K·N1M1 = N1A·N1B. Таким образом, степени точки N1 относительно окружностей Ω и ω2 равны, то есть N1 лежит на прямой M2Y2. Аналогично N2 лежит на прямой M1Y1 (см. рис.). Но четырёхугольник M1M2N2N1, очевидно, вписанный, откуда и следует требуемое равенство.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь