Доказательство расположения жуках на плоскости

Решение 1:   Пусть два жука дружат тогда и только тогда, когда соответствующие точки на рисунке соединены сплошным отрезком.

  Легко видеть, что расположить жуков на плоскости так, чтобы расстояние между любыми двумя друзьями равнялось 1, можно только изображённым на рисунке способом. Но тогда пунктирный отрезок тоже равен 1, а соединенные им жуки друзьями не являются. С другой стороны, если удалить любого жука, то можно повернуть часть рисунка вокруг одной из соседних точек, обеспечив выполнение условий задачи.

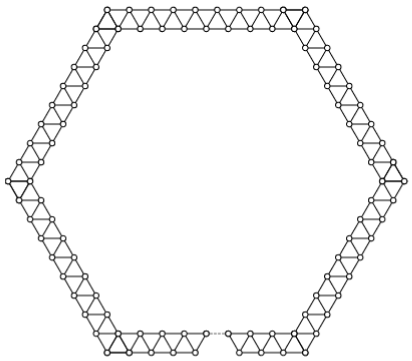
Решение 2:Рассмотрим следующий граф: трапеция ABCD с основаниями  BC = 33  и  AD = 34  высоты    составленная из 67 правильных треугольников со стороной 1, и A и D соединены путем длины 33. Очевидно, его нельзя нарисовать на плоскости, соблюдая условие задачи, а граф, полученный из него удалением любой вершины, можно.

Неверно.