Назад
Задача 166264 • Сложность: 2 • 8-10 класс
Задача

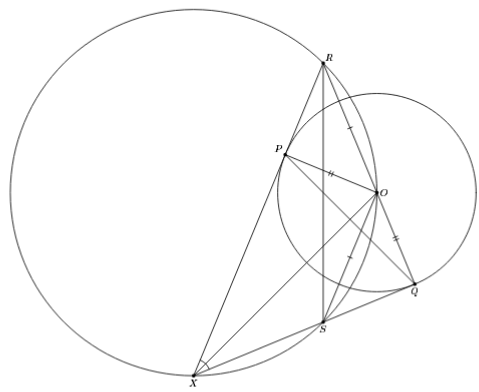
Центр окружности ω2 лежит на окружности ω1. Из точки X окружности ω1 проведены касательные XP и XQ к окружности ω2 (P и Q – точки касания), которые повторно пересекают ω1 в точках R и S. Докажите, что прямая PQ проходит через середину отрезка RS.

Авторы:
Нилов Ф.
Разделы:
Планиметрия
Источники:
Олимпиады и турниры Олимпиада по геометрии имени И.Ф. Шарыгина XII Олимпиада по геометрии имени И.Ф. Шарыгина (2016 г.)
Количество версий:
4
Решение

Пусть O – центр ω2. Так как XO – биссектриса угла PXQ, то  OR = OS. Первый способ. Прямоугольные треугольники OPR и OQS равны по катету и гипотенузе, то есть  PR = QS  (см. рис.). Поскольку  ∠;XPQ = ∠XQP,  то точки R и S равноудалены от прямой PQ, что равносильно утверждению задачи.

Второй способ. Середина K отрезка RS – это проекция O на прямую RS. Точки P, Q и K лежат на одной прямой – прямой Симсона точки O (см. задачу 152421.
Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет