Задача
Дан квадрат ABCD. Первая окружность касается сторон угла A, вторая – сторон угла B, причём сумма диаметров окружностей равна стороне квадрата. Докажите, что одна из общих касательных этих окружностей пересекает сторону AB в её середине.
Решение
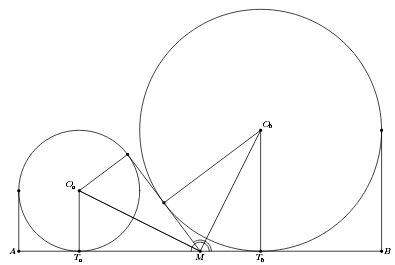
Пусть Oa, Ob – центры окружностей, Ta, Tb – точки их касания с AB, M – середина AB (см. рис.). Из условия следует, что TaM = TbOb, TbM = TaOa. Следовательно, прямоугольные треугольники OaTaM и MTbOb равны, а OaM ⊥ ObM. Значит, прямая l, симметричная AB относительно OaM, будет также симметрична AB относительно ObM. Поскольку расстояния от центров окружностей до l равны их радиусам, l – общая касательная.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет