Задача
Точка D лежит на основании BC равнобедренного треугольника ABC, а точки M и K – на его боковых сторонах AB и AC соответственно, причём AMDK – параллелограмм. Прямые MK и BC пересекаются в точке L. Перпендикуляр к BC, восставленный из точки D, пересекает прямые AB и AC в точках X и Y соответственно. Докажите, что окружность с центром L, проходящая через D, касается описанной окружности треугольника AXY.
Решение
Описанные окружности Ω и ω треугольников ABC и AXY, очевидно, перпендикулярны. Пусть E – вторая точка их пересечения. Рассмотрим на Ω точку A', диаметрально противоположную точке A и поворотную гомотетию с центром E, переводящую A в A'. Тогда она переводит треугольник XAY в треугольник BA'C. Поэтому (прямоугольные) треугольники EXB и EYC подобны, то есть EB : EC = XB : YC = BD : CD. С другой стороны,
LB : LD = LM : LK = LD : LC. Поэтому точки B и C инверсны относительно окружности Ω' с центром L и радиусом LD и Ω' также перпендикулярна Ω. Кроме того, для всех точек окружности Ω' отношение расстояний до B и C одно и то же (окружность Аполлония), а значит, она проходит через E (см. рис.). Таким образом, обе окружности ω и Ω' перпендикулярны окружности Ω и пересекают её в одной точке. Следовательно, они касаются.
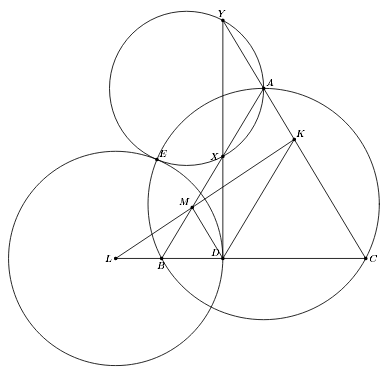
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь