Пересечение диагоналей и свойство параллелограммов
Задача
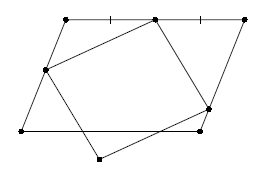
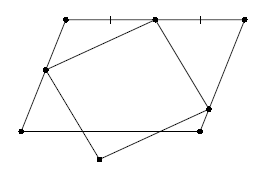
Два параллелограмма расположены так, как показано на рисунке. Докажите, что диагональ одного параллелограмма проходит через точку пересечения диагоналей другого.
Решение
Введем обозначения (см. рисунок). Докажем, что отрезок KL проходит через O – точку пересечения диагоналей параллелограмма ABCD. Заметим, что O – середина отрезка BD, то есть KO – средняя линия треугольника CBD. Тогда достаточно доказать параллельность прямых KL и CD. Пусть Q – точка пересечения диагоналей параллелограмма MKPL. Тогда KQ – средняя линия трапеции MBCP, то есть параллельна ее основаниям. Следовательно, прямые KL и CD параллельны, что и требовалось.
Источники и прецеденты использования
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет