Задача по стереометрии и комбинаторной геометрии о N-угольниках
Задача
Известно, что если у правильного $N$-угольника, находящегося внутри окружности, продлить все стороны до пересечения с этой окружностью, то $2N$ добавленных к сторонам отрезков можно разбить на две группы с одинаковой суммой длин. А верно ли аналогичное утверждение для находящегося внутри сферы
а) произвольного куба;
б) произвольного правильного тетраэдра?
(Каждое ребро продлевают в обе стороны до пересечения со сферой. В итоге к каждому ребру добавляется по отрезку с обеих сторон. Требуется покрасить каждый из них либо в красный, либо в синий цвет, чтобы сумма длин красных отрезков была равна сумме длин синих.)
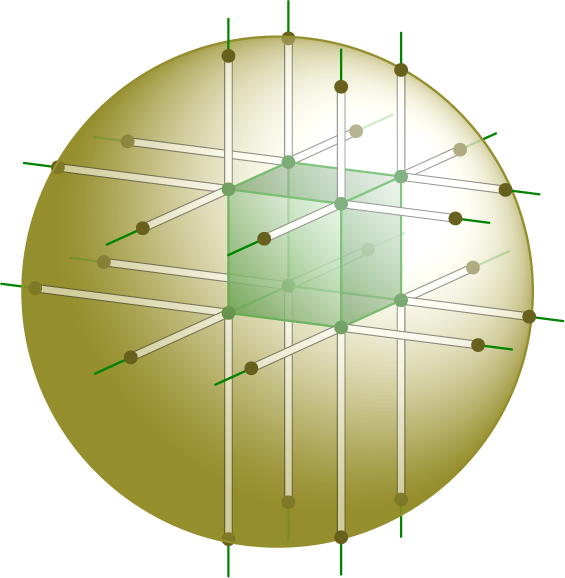
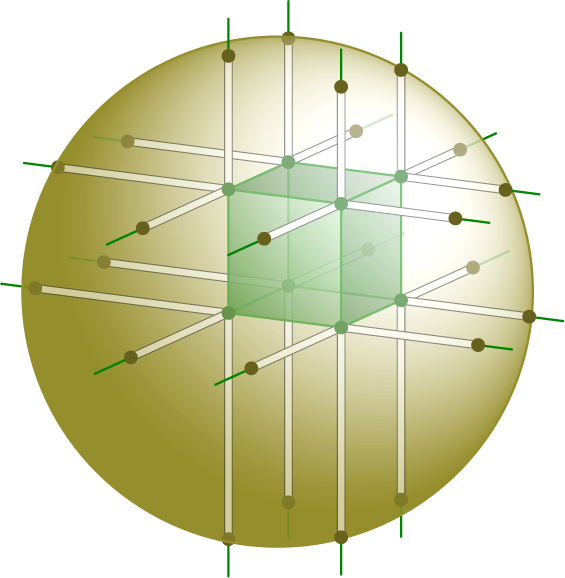
Решение
а) Посмотрим сначала на горизонтальные отрезки. Они получаются
продолжением сторон квадратов (верхней и нижней грани куба) внутри
кругов. Поэтому их можно разбить на две группы с одинаковой суммой.
Достаточно теперь разбить на две группы с одинаковой суммой 8
вертикальных отрезков. Посмотрим на 4 из них, лежащие в одной плоскости. Мы видим квадрат $ABCD$ внутри круга, стороны $AB$ и $CD$
которого продлили до пересечения с этим кругом (точки $A’$, $B’$, $C’$, $D’$).
 Докажем, что $AA’+CC’=BB’+DD’$. Общий перпендикуляр $l$ к хордам $A’B’$ и $C’D’$ – ось симметрии окружности. Поэтому если $l$ является осью симметрии и квадрата, то утверждение очевидно. А иначе – сдвинем
квадрат вдоль наших хорд так, чтобы $l$ стал его осью симметрии – если
при этом $AA’$ и $DD’$ увеличиваются на $x$, то $BB’$ и $CC’$ на $x$ уменьшаются, поэтому на равенство такой сдвиг не влияет.
Докажем, что $AA’+CC’=BB’+DD’$. Общий перпендикуляр $l$ к хордам $A’B’$ и $C’D’$ – ось симметрии окружности. Поэтому если $l$ является осью симметрии и квадрата, то утверждение очевидно. А иначе – сдвинем
квадрат вдоль наших хорд так, чтобы $l$ стал его осью симметрии – если
при этом $AA’$ и $DD’$ увеличиваются на $x$, то $BB’$ и $CC’$ на $x$ уменьшаются, поэтому на равенство такой сдвиг не влияет.
Итак, мы разделили наши отрезки на несколько групп (две группы горизонтальных отрезков и две группы вертикальных отрезков), каждую из которых разбили на две «половины» с одинаковыми суммами длин. Утверждение пункта а) доказано.
б) Если у тетраэдра одна вершина в центре сферы, а три другие лежат на её поверхности, отрезков фактически три и все равны радиусу сферы $r$. Три равных отрезка нельзя разбить на две группы с равными суммами длин: в одной из групп будет «перевес» хотя бы на целый радиус.
И даже если три другие вершины лежат не на самой сфере, но близко к ней, то длины всех девяти исходящих из них отрезков не смогут покрыть «перевес» в радиус между двумя группами. Проведем точную оценку: если ребро тетраэдра равно $a$, то три вершины лежат на сфере радиуса $a < r$. Тогда любой из девяти выходящих из них отрезков не превосходит $\sqrt{r^2-a^2}$ (например, это следует из теоремы о касательной и секущей). Осталось подобрать радиус $a$ так, что $9 \sqrt{r^2-a^2} < r$. Это выполняется при $ a > \sqrt \frac{80}{81} r$.
Ответ
Для куба утверждение верно, для правильного тетраэдра – не верно.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь