Задача
На стороне $AB$ квадрата $ABCD$ вне его построен равнобедренный треугольник $ABE$ ($AE=BE$). Пусть $M$ – середина $AE$, $O$ – точка пересечения $AC$ и $BD$, $K$ – точка пересечения $ED$ и $OM$. Докажите, что $EK=KO$.
Решение
Так как $OM$ – средняя линия треугольника $ACE$, $OM\parallel EC$, следовательно, $\angle KOE=\angle OEC$. Но очевидно, что $EO$ – биссектриса угла $CED$. Значит, $\angle EOK=\angle OEK$ и треугольник $OKE$ – равнобедренный.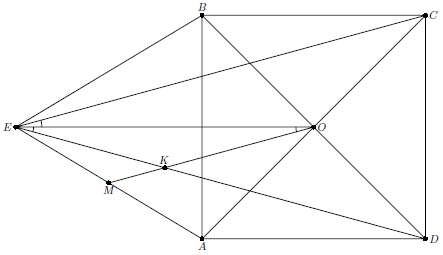 
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет