Олимпиадная задача: перпендикуляр в треугольнике $ABC$
Задача
Точка $O$ – центр описанной окружности остроугольного треугольника $ABC$, $AH$ – его высота. Точка $P$ – основание перпендикуляра, опущенного из точки $A$ на прямую $CO$. Докажите, что прямая $HP$ проходит через середину стороны $AB$.
Решение
$\angle B = \frac{1}{2}\angle AOC$ = 90° – $\angle OCA = \angle PAC =\angle PHB$ (последнее равенство следует из очевидной вписанности четырёхугольника $APHC$). Значит, луч $HP$ отсекает от прямоугольного треугольника $ABH$ равнобедренный треугольник $BMH$. Поэтому $M$ – середина $AB$. 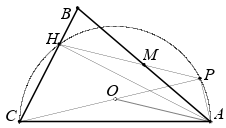
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет