Задача
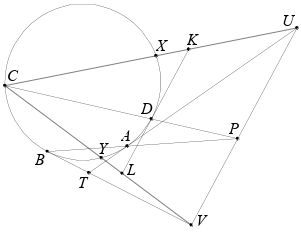
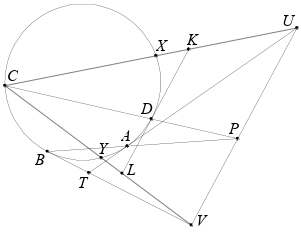
Четырёхугольник $ABCD$ вписан в окружность. Лучи $BA$ и $CD$ пересекаются в точке $P$. Прямая, проходящая через $P$ и параллельная касательной к окружности в точке $D$, пересекает в точках $U$ и $V$ касательные, проведённые к окружности в точках $A$ и $B$. Докажите, что окружности, описанные около треугольника $CUV$ и четырёхугольника $ABCD$, касаются.
Решение
Пусть лучи $UC$ и $VC$ пересекают в точках $K$ и $L$ касательную, проведённую из точки $D$, и вторично окружность в точках $X$ и $Y$ (см. рис.). Пусть $T$ – общая точка касательных, проведённых из $A$ и $B$. Запишем теорему Менелая для треугольника $UVT$ и прямой $BP$: $\dfrac{UP}{PV} \cdot\dfrac{VB}{BT}\cdot\dfrac{TA}{AU} = 1$. Учитывая, что $BT = TA$ и $\dfrac{UP}{PV} = \dfrac{KD}{DL}$, получаем $\dfrac{KD\cdot VB}{DL\cdot AU}=1$ (если точка $T$ не существует, то это равенство очевидно), то есть $\dfrac{UA}{KD} = \dfrac{VB}{LD}$. По теореме о секущей и касательной $\dfrac{UX\cdot UC}{KX \cdot KC} = \dfrac{UA ^2}{KD^2} = \dfrac{VB^2}{LD^2} = \dfrac{VY\cdot VC}{LY \cdot LC}$. Поскольку $\dfrac{UC}{KC} = \dfrac{VC}{LC}$, то $\dfrac{UX}{KX} = \dfrac{VY}{LY}$.
Следовательно, по обратной теореме Фалеса прямые $XY$ и $UV$ параллельны. Поэтому существует гомотетия с центром $C$, переводящая треугольник $CXY$ в треугольник $CUV$. Значит, их описанные окружности касаются в точке $C$, что и требовалось.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь