Пусть (n–1)-я перевёрнутая монета – $X$, а $n$-я – $Y$. Тогда между $X$ и $Y$ по часовой стрелке лежит  $n - 1$  монета, а раз всего монет в круге  $2n + 1$,  то между $Y$ и Х по часовой стрелке лежит $n$ монет (см. рисунок). Это значит, что (n+1)-й мы снова перевернём монету $X$.

  И далее мы будем переворачивать уже переворачивавшиеся монеты, но в обратном порядке: ведь пропустить по часовой стрелке  $n + 1$  монету – всё равно, что пропустить против часовой стрелки  $n - 2$ монеты, ..., пропустить по часовой стрелке  $2n - 2$  монеты – всё равно, что пропустить против часовой стрелки 1 монету. А на последних двух шагах мы перевернём одну и ту же монету.

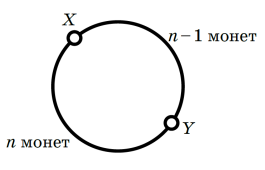
  В итоге решкой вверх будет лежать только монета $Y$ – она переворачивалась нечётное число раз, а все остальные монеты – чётное.

Ответ задачи отсутствует