Задачи и олимпиады по математике

Задача

В прямоугольник $ABCD$ вписывают равнобедренные треугольники с заданным углом α при вершине, противолежащей основанию, так, что эта вершина лежит на отрезке $BC$, а концы основания – на отрезках $AB$ и $CD$. Докажите, что середины оснований у всех таких треугольников совпадают.

Решение

Пусть $KLM$ – один из таких треугольников, $O$ – середина его основания KM (см. рисунок).

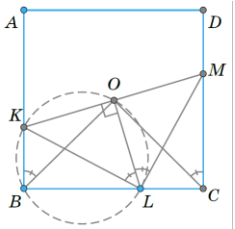
Тогда $LO$ – медиана, а значит, и биссектриса, и высота треугольника $KLM$. Поскольку углы $KBL$ и $LOK$ прямые, точки $B$ и $O$ лежат на окружности c диаметром $KL$, откуда $\angle KBO = \angle KLO$ = ^α/₂. Аналогично ∠МСO = ∠МLO = ^α/₂. Следовательно, $O$ – точка пересечения фиксированных прямых, проведённых из вершин $B$ и $C$, то есть она не зависит от положения треугольника $KLM$.

Ответ

Ответ задачи отсутствует

Задача

Решение

Ответ

Подтверждение удаления