Задание по олимпиадной математике: Сторона шестиугольника
Задача
Расстояние от некоторой точки внутри правильного шестиугольника до трёх его последовательных вершин равны 1, 1 и 2 соответственно.
Чему равна сторона этого шестиугольника?
Решение
Пусть $A, B, C$ – последовательные вершины шестиугольника, $O$ – точка внутри него, $OA = OB = 1, OC = 2$. Первый способ. Рассмотрим другую соседнюю с $A$ вершину $F$. Тогда $FABC$ – равнобедренная трапеция (рис. слева). Точка $O$ лежит на общем серединном перпендикуляре её оснований $FC$ и $AB$, поэтому $OF = OC = 2$. Иак как при этом $FC = 2AB$ , треугольники $AOB$ и $FOC$ подобны с коэффициентом 2. Поскольку точка $O$ – центр гомотетии, переводящей один из этих треугольников в другой, она лежит на диагонали $AC$ (аналогично она лежит на диагонали $BF$). Тогда $\angle OBC = 120^{\circ} - 30^{\circ} = 90^{\circ}$, и $BC = \sqrt{2^2-1^2} = \sqrt{3}$ .
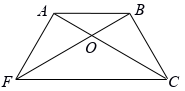
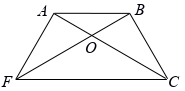
Ответ
$\sqrt{3}$.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь