Угол многоугольника и треугольники
Задача
Любые три последовательные вершины невыпуклого многоугольника образуют прямоугольный треугольник. Обязательно ли у многоугольника найдется угол, равный $90$ или $270$ градусам?
Решение
Решение 1:Возьмем прямоугольник со сторонами $2$ и $\sqrt{3}$ и построим на каждой из его сторон во внешнюю сторону трапецию с отношением сторон $1:1:1:2$, меньшее основание которой совпадает со стороной прямоугольника. Любые три последовательные вершины полученного невыпуклого двенадцатиугольника образуют треугольник с углами $30^{\circ}$, $60^{\circ}$ и $90^{\circ}$, а углы двенадцатиугольника равны $60^{\circ}$ или $330^{\circ}$.
Решение 2:
Пусть $A=(0,1)$, $B=(1,0)$, $C=(1,1)$, $D=(2,0)$, $E=(2,1)$, $F=(3, 0)$, а $G$ – точка пересечения $BE$ с прямой, проходящей через $F$ и перпендикулярной $AF$. Тогда семиугольник $ABCDEFG$ – искомый.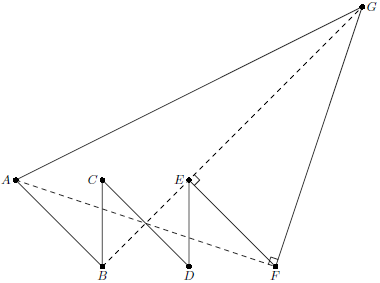
Ответ
Нет.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет